Producte vectorial de dos vectors
Producte vectorial de dos vectors
Donats dos vectors \(\vec{u}=\left(u_1,u_2,u_3\right)\) i \(\vec{v}=\left(v_1,v_2,v_3\right)\), s'anomena producte vectorial, i es simbolitza \(\vec{u}\times\vec{v}\), el vector obtingut de l'expressió:
\(
\begin{align}
\vec{u}\times\vec{v}
&=\left|\begin{array}{ccc}
\vec{e}_1 & u_1 & v_1 \\
\vec{e}_2 & u_2 & v_2 \\
\vec{e}_3 & u_3 & v_3
\end{array}\right| \\[10pt]
&=\left(u_2v_3-u_3v_2\right)\vec{e}_1+\left(u_3v_1-u_1v_3\right)\vec{e}_2+\left(u_1v_2-u_2v_1\right)\vec{e}_3 \\[10pt]
&=\left(u_2v_3-u_3v_2,\, u_3v_1-u_1v_3,\,u_1v_2-u_2v_1\right)
\end{align}
\)
Observacions:
El producte vectorial de dos vectors és un vector.
L'expressió per calcular el producte vectorial de dos vectors no és un determinant perquè la seva primera columna està formada per vectors i no per nombres reals, i també perquè el seu resultat final no és un nombre real sinó que és un vector. Tot i això s'escriu i es calcula com si fos un determinant.
Si els vectors \(\vec{u}\) i \(\vec{v}\) són linealment independents, aleshores el producte vectorial \(\vec{u}\times\vec{v}\) és un vector perpendicular a tots dos.
Si els vectors \(\vec{u}\) i \(\vec{v}\) són linealment dependents, aleshores el producte vectorial \(\vec{u}\times\vec{v}\) és el vector nul \(\vec{0}\).
Com a cas particular \(\vec{u}\times\vec{u}=\vec{0}\).
Exercici 32
Donats els vectors \(\vec{u}=(5,1,3)\) i \(\vec{v}=(-2,0,1)\), calcula el vector \(\vec{w}=\vec{u}\times\vec{v}\) i comprova que és perpendicular a \(\vec{u}\) i \(\vec{v}\).
| Solució: |
\(\vec{w}=(1,-11,2)\), \(\vec{u}\cdot\vec{w}=0\), \(\vec{v}\cdot\vec{w}=0\) |
Mòdul i sentit del producte vectorial
El mòdul del producte vectorial de dos vectors \(\vec{a}\) i \(\vec{b}\) es calcula amb l'expressió:
\(\left|\vec{a}\times\vec{b}\right|=\left|\vec{a}\right|\left|\vec{b}\right|\sin\alpha\)
on \(\alpha\) és el més petit dels dos angles \(\vec{a}\) i \(\vec{b}\).
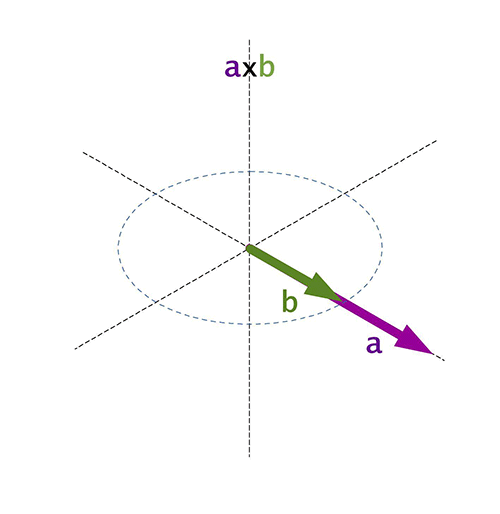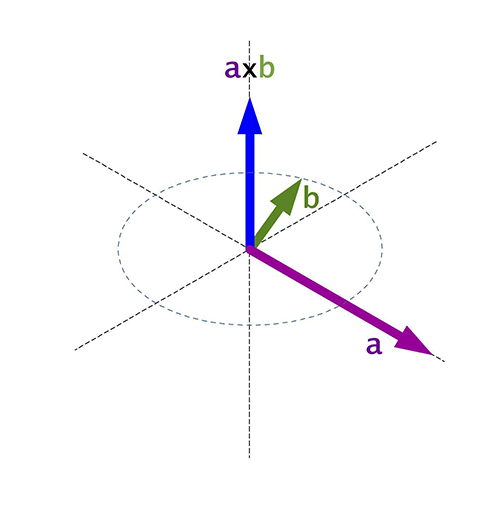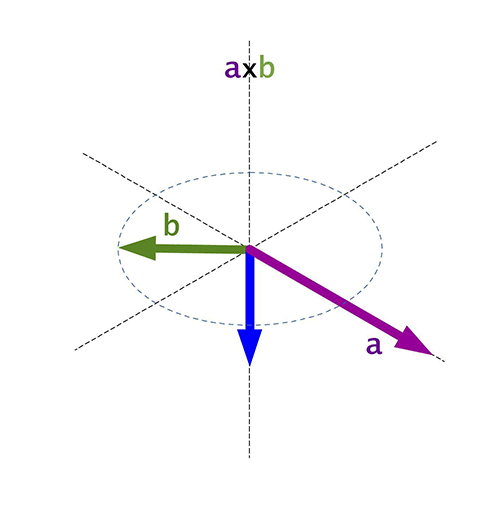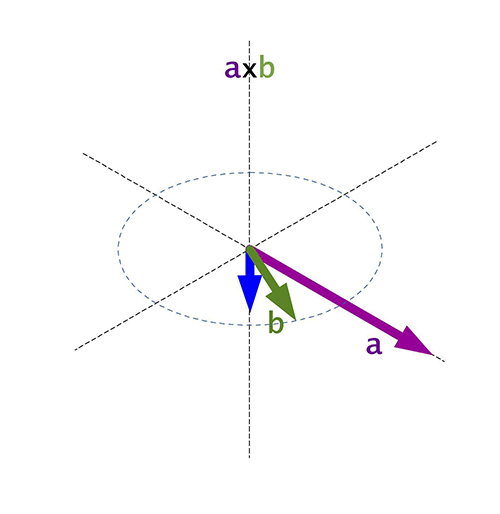
El sentit és el d'avanç d'un tirabuixó que giri del vector \(\vec{a}\) al vector \(\vec{b}\) segons el menor angle possible. Aquesta direcció també es pot trobar amb la regla de la mà dreta.
Exercici 33
Donats els vectors \(\vec{u}=(3,-2,1)\) i \(\vec{v}=(1,1,4)\),
| a) calcula \(\vec{u}\times\vec{v}\) |
Solució: |
\(\vec{u}\times\vec{v}=(-9,-11,5)\) |
| b) i calcula el més petit dels dos angles que formen. |
Solució: |
\(\alpha\approx\textrm{71,641}^{\circ}\) |
Exercici 34
Determina tots els vectors de mòdul \(15\) que són ortogonals als vectors \(\vec{a}=(-2,1,2)\) i \(\vec{b}=(2,1,-6)\).
| Solució: |
\((10,10,5)\) i \((-10,-10,-5)\) |
Propietats algebraiques del producte vectorial de dos vectors
-
Anticommutativa:
\(\vec{u}\times\vec{v}=-\vec{v}\times\vec{u}\)
-
Distributiva respecte a la suma de vectors:
\(\vec{u}\times\left(\vec{v}+\vec{w}\right)=\vec{u}\times\vec{v}+\vec{u}\times\vec{w}\)
-
Associativa del producte d'un nombre real pel producte vectorial de dos vectors:
\(k\,(\vec{u}\times\vec{v})=(k\,\vec{u})\times\vec{v}=\vec{u}\times(k\,\vec{v})\)
Exercici 35
Calcula els següents productes vectorials:
| \(\vec{e}_1\times\vec{e}_1=\) |
\(\vec{e}_1\times\vec{e}_2=\) |
\(\vec{e}_1\times\vec{e}_3=\) |
| \(\vec{e}_2\times\vec{e}_1=\) |
\(\vec{e}_2\times\vec{e}_2=\) |
\(\vec{e}_2\times\vec{e}_3=\) |
| \(\vec{e}_3\times\vec{e}_1=\) |
\(\vec{e}_3\times\vec{e}_2=\) |
\(\vec{e}_3\times\vec{e}_3=\) |
| \(\vec{e}_1\times\vec{e}_1=\vec{0}\) |
\(\vec{e}_1\times\vec{e}_2=\vec{e}_3\) |
\(\vec{e}_1\times\vec{e}_3=-\vec{e}_2\) |
| \(\vec{e}_2\times\vec{e}_1=-\vec{e}_3\) |
\(\vec{e}_2\times\vec{e}_2=\vec{0}\) |
\(\vec{e}_2\times\vec{e}_3=\vec{e}_1\) |
| \(\vec{e}_3\times\vec{e}_1=\vec{e}_2\) |
\(\vec{e}_3\times\vec{e}_2=-\vec{e}_1\) |
\(\vec{e}_3\times\vec{e}_3=\vec{0}\) |
Solució:
Exercici 36
Donats els vectors \(\vec{a}=(5,-1,0)\), \(\vec{b}=(1,1,2)\) i \(\vec{c}=(4,0,-2)\), comprova si es verifica la propietat associativa.
\(\vec{a}\times\left(\vec{b}\times\vec{c}\right)=\left(\vec{a}\times\vec{b}\right)\times\vec{c}\)
Solució:
No es verifica la propietat associativa
\( \vec{a}\times\left(\vec{b}\times\vec{c}\right) = (4,20,48) \)
\( \left(\vec{a}\times\vec{b}\right)\times\vec{c} = (20,20,40) \)
\( \vec{a}\times\left(\vec{b}\times\vec{c}\right) \ne \left(\vec{a}\times\vec{b}\right)\times\vec{c} \)
Exercici 37
Donats els vectors \(\vec{a}=(0,1,-2)\), \(\vec{b}=(-1,3,-1)\) i \(\vec{c}=(2,0,1)\), calcula l'expressió:
\(\vec{a}\times\left(\vec{b}\times\vec{c}\right) + \vec{b}\times\left(\vec{c}\times\vec{a}\right) + \vec{c}\times\left(\vec{a}\times\vec{b}\right)\)
Propietats geomètriques del producte vectorial de dos vectors
Àrea d'un paral·lelogram
El mòdul del producte vectorial de dos vectors es pot interpretar com l'àrea del paral·lelogram que té per costats els vectors \(\vec{a}\) i \(\vec{b}\).
\(A=\left|\vec{a}\right|\,h=\left|\vec{a}\right|\,\left|\vec{b}\right|\,\sin\alpha=\left|\vec{a}\times\vec{b}\right|\)
Àrea d'un triangle
\(\displaystyle A=\frac{1}{2}\,\left|\vec{a}\times\vec{b}\right|=\frac{1}{2}\,\left|\vec{PQ}\times\vec{PR}\right|\)
Exercici 38
Els punts \(A(3,4,2)\), \(B(4,0,1)\) i \(C(5,6,5)\) són tres vèrtexs consecutius d'un paral·lelogram. Calcula la seva àrea.
Exercici 39
Els punts \(A(0,1,2)\), \(B(4,0,1)\) i \(C(5,6,5)\) són els tres vèrtexs d'un triangle. Calcula la seva altura sobre el costat \(AB\).