Binomi de Newton
Potències d'un binomi
Les identitats notables son expressions algebraiques que convé conèixer per la seva utilitat. Les de grau \(2\) són:
\(\displaystyle \begin{array}{rcl} (a+b)^2 &=& a^2+2ab+b^2 \\ (a-b)^2 &=& a^2-2ab+b^2 \\ (a+b)(a-b) &=& a^2-b^2\end{array}\)
Les dues primeres s'anomenen quadrat d'un binomi i es poden resumir en una sola.
\(\displaystyle (a \pm b)^2 = a^2 \pm 2ab +b^2 \)
Exercici 9:
Efectua les següents operacions aplicant les identitats notables:
| a) \( \Big(3x+5\Big)^2 \) |
Solució: |
\(9x^2+30x+25\)
|
| b) \(\Big(x-\sqrt{3}\Big)^2\) |
Solució: |
\(x^2-2\sqrt{3}x+3\)
|
| c) \(\Big(2x^3+3x^2\Big)^2\) |
Solució: |
\(4x^6+12x^5+9x^4\)
|
| d) \(\Big(\sqrt{5}x-\sqrt{2}\Big)^2\) |
Solució: |
\(5x^2-2\sqrt{10}x+2\)
|
| e) \(\Big(5x^2+3x\Big)\cdot\Big(5x^2-3x\Big)\) |
Solució: |
\(25x^4-9x^2\)
|
Exercici 10:
Expressa en forma de binomi al quadrat o de “suma per diferència”:
| a) \( x^2+14x+49 \) |
Solució: |
\(\Big(x+7\Big)^2\)
|
| b) \( x^2-6x+9 \) |
Solució: |
\(\Big(x-3\Big)^2\)
|
| c) \( 9x^2+12x+4 \) |
Solució: |
\(\Big(3x+2\Big)^2\)
|
| d) \( 9x^4+30x^2+25 \) |
Solució: |
\(\Big(3x^2+5\Big)^2\)
|
| e) \(\displaystyle x^2-5x+\frac{25}{4} \) |
Solució: |
\(\displaystyle\Bigg(x-\frac{5}{2}\Bigg)^2\)
|
| f) \( 2x^2 - 8x + 8 \) |
Solució: |
\(\Big(\sqrt{2}x-\sqrt{8}\Big)^2\)
|
| g) \( 25x^2 - 16 \) |
Solució: |
\(\Big(5x+4\Big)\cdot\Big(5x-4\Big)\)
|
| h) \( x^6 - 9x^4 \) |
Solució: |
\(\Big(x^3+3x^2\Big)\cdot\Big(x^3-3x^2\Big)\)
|
Existeixen fórmules semblants per a qualsevol potència d'un binomi amb exponent natural.
Exemple:
Si desenvolupem l'expressió \((a+b)^3\):
\(\displaystyle
\begin{align}
(a+b)^3
&= (a+b)\cdot(a+b)^2 \\[6pt]
&= (a+b)\cdot(a^2+2ab+b^2) \\[6pt]
&= a^3+2a^2b+ab^2+a^2b+2ab^2+b^3 \\[6pt]
&= a^3+3a^2b+3ab^2+b^3
\end{align}
\)
arribem a la identitat notable que ens permet calcular el cub d'un binomi:
\(\displaystyle (a+b)^3 = a^3+3a^2b+3ab^2+b^3 \)
Exercici 11:
Fes servir la identitat notable \(\displaystyle (a+b)^3 = a^3+3a^2b+3ab^2+b^3\) per desenvolupar l'expressió \(\displaystyle (2x+5)^3\).
Solució:
\(\displaystyle
\begin{align}
(2x+5)^3
&= (2x)^3+3\cdot(2x)^2\cdot5+3\cdot(2x)\cdot5^2+5^3 \\[6pt]
&= 8x^3+3\cdot4x^2\cdot5+3\cdot2x\cdot25+125 \\[6pt]
&= 8x^3+60x^2+150x+125
\end{align}
\)
Exercici 12:
Troba la identitat notable correponent a l'expressió \((a-b)^3\).
Solució:
\(\displaystyle (a-b)^3 = a^3-3a^2b+3ab^2-b^3 \)
Exercici 13:
Troba la identitat notable correponent a l'expressió \((a+b)^4\).
Solució:
\(\displaystyle (a+b)^4 = a^4+4a^3b+6a^2b^2+4ab^3+b^4 \)
Els coeficients que resulten de desenvolupar el binomi de Newton s'anomenen coeficients binomials. Per exemple en la identitat notable \(\displaystyle (a+b)^2 = a^2+2ab+b^2\) els coeficients binomials són \(1\), \(2\) i \(1\), i en la identitat notable \(\displaystyle (a+b)^3 = a^3+3a^2b+3ab^2+b^3\) són \(1\), \(3\), \(3\) i \(1\). Aquests coeficients es podran calcular d'una manera més senzilla fent servir els nombres factorials.
Factorial d'un nombre
El factorial d'un nombre natural \(n\) es defineix com el producte de tots els nombres naturals des de \(1\) fins a \(n\). S'escriu \(n!\) i es llegueix "n factorial".
\(\displaystyle n! = 1 \cdot 2 \cdot 3 \cdot \ldots \cdot (n-1) \cdot n = \prod_{i=1}^{n} i \)
Per exemple:
\(5! = 1 \cdot 2 \cdot 3 \cdot 5 \cdot 5 = 120\)
Aquesta definició només és vàlida per a nombres naturals. Per al nombre zero el factorial es defineix:
\(\displaystyle 0! = 1 \)
Exercici 14:
Completa la següent taula.
\(\displaystyle
\begin{array}{c|c}
\phantom{0}n\phantom{0}&n!\\[5pt]\hline
0&1\\[5pt]
1&1\\[5pt]
2&2\\[5pt]
3&6\\[5pt]
4&24\\[5pt]
5&120\\[5pt]
6&720\\[5pt]
7&5040\\[5pt]
8&40320\\[5pt]
9&362880
\end{array}
\)
\(\displaystyle
\begin{array}{c|c}
\phantom{0}n\phantom{0}&n!\\[5pt]\hline
0&\\[5pt]
1&\\[5pt]
2&\\[5pt]
3&\\[5pt]
4&\\[5pt]
5&\\[5pt]
6&\\[5pt]
7&\\[5pt]
8&\\[5pt]
9&\phantom{362880}
\end{array}
\)
Solució:
Exercici 15:
Calcula els següents nombres:
| a) \( (4 \cdot 3)! \) |
Solució: |
\(479001600\)
|
| b) \( 4! \cdot 3! \) |
Solució: |
\(144\)
|
| c) \( (8+7)! \) |
Solució: |
\(1307674368000\)
|
| d) \( 8!+7! \) |
Solució: |
\(45360\)
|
| e) \( \displaystyle \frac{10!}{7!} \) |
Solució: |
\(720\)
|
| f) \( \displaystyle \frac{20!}{15!} \) |
Solució: |
\(1860480\)
|
| g) \( \displaystyle \frac{1000!}{997!} \) |
Solució: |
\(997002000\)
|
Coeficients binomials
Es defineix el coeficient binomial \(\displaystyle \binom{n}{k}\) com el coeficient del monomi \(a^k\) en el desenvolupament del binomi \((a+b)^n\). Per exemple en la identitat notable \(\displaystyle (a+b)^3 = a^3+3a^2b+3ab^2+b^3\) els coeficients binomials són:
\(\displaystyle \binom{3}{0}=1\,\), \(\displaystyle \;\binom{3}{1}=3\,\), \(\displaystyle \;\binom{3}{2}=3\,\;\) i \(\displaystyle \;\binom{3}{3}=1\)
Aquests coeficients són nombres naturals que es poden calcular amb la següent expressió:
\(\displaystyle \binom{n}{k} = \frac{n!}{k! \cdot (n-k)!} \)
on \(n\) i \(k\) són enters no negatius, i a més es verifica que \(k \le n\).
Els coeficients binomials s'anomenen també nombres combinatoris, i s'escriuen \(C_{n,k}\).
Exercici 16:
Calcula, simplificant prèviament, els següents coeficients binomials:
| a) \( \displaystyle \binom{7}{4} \) |
Solució: |
\(\displaystyle \binom{7}{4}=\frac{7!}{4!·3!}=\frac{7·6·5·\bcancel{4!}}{\bcancel{4!}·3·2·1}=35\)
|
| b) \( \displaystyle \binom{9}{2} \) |
Solució: |
\(\displaystyle \binom{9}{2}=\frac{9!}{2!·7!}=\frac{9·8·\bcancel{7!}}{2·1·\bcancel{7!}}=36\)
|
| c) \( \displaystyle \binom{9}{7} \) |
Solució: |
\(\displaystyle \binom{9}{7}=\frac{9!}{7!·2!}=\frac{9·8·\bcancel{7!}}{\bcancel{7!}·2·1}=36\)
|
| d) \( \displaystyle \binom{12}{0} \) |
Solució: |
\(\displaystyle \binom{12}{0}=\frac{12!}{0!·12!}=\frac{\bcancel{12!}}{1·\bcancel{12!}}=1\)
|
| e) \( \displaystyle \binom{8}{8} \) |
Solució: |
\(\displaystyle \binom{8}{8}=\frac{8!}{8!·0!}=\frac{\bcancel{8!}}{\bcancel{8!}·1}=1\)
|
| f) \( \displaystyle \binom{17}{1} \) |
Solució: |
\(\displaystyle \binom{17}{1}=\frac{17!}{1!·16!}=\frac{17·\bcancel{16!}}{1·\bcancel{16!}}=17\)
|
| g) \( \displaystyle \binom{500}{3} \) |
Solució: |
\(\displaystyle \binom{500}{3}=\frac{500!}{3!·497!}=\frac{500·499·498·\bcancel{497!}}{3·2·1·\bcancel{497!}}=20708500\)
|
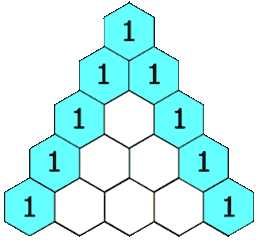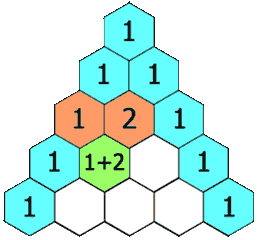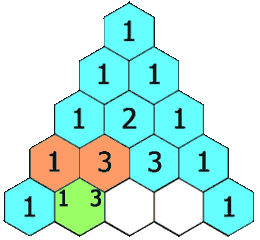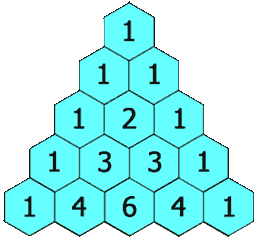
Els coeficients binomials es poden disposar formant un triangle que es coneix com a Triangle de Tartaglia. L'índex \(n\) indica la fila, començant per la fila \(0\), i l'índex \(k\) la posició dins de la fila, començant per la posició \(0\).
Propietats dels coficients binomials
-
Els coeficients binomials són nombres naturals.
-
Identitat de Pascal
\(\displaystyle \binom{n}{k} = \binom{n-1}{k-1}+\binom{n-1}{k} \)
-
Simetria dels coeficients
\(\displaystyle \binom{n}{k} = \binom{n}{n-k} \)
-
El primer i l'últim coeficient de cada fila són iguals a \(1\)
\(\displaystyle \binom{n}{0} = \binom{n}{n} = 1 \)
-
El segon i el penúltim coeficient de la fila \(n\) són iguals a \(n\)
\(\displaystyle \binom{n}{1} = \binom{n}{n-1} = n \)
-
La suma de tots els coeficients de la fila \(n\) és igual a \(2^n\)
\(\displaystyle \sum_{i=0}^{n} \binom{n}{i} = 2^n \)
Fórmula del binomi de Newton
\(\displaystyle \begin{align} (a+b)^n &= \sum_{i=1}^{n} \binom{n}{i}a^{n-i}b^i \\[6pt] &= \binom{n}{0}a^{n} + \binom{n}{1}a^{n-1}b + \binom{n}{2}a^{n-2}b^2 + \ldots + \binom{n}{n}b^n \end{align} \)
En el cas de les restes \((a-b)^n\) simplement canviarem el signe dels termes amb potències de \(b\) d'exponent senar.
Com a exemple, la fórmula del binomi de Newton, \((a+b)^n\) per a valors de \(n\) des de \(0\) fins a \(4\) queda de la següent forma:
\(\displaystyle \begin{array}{rcl} (a+b)^0 &=& 1\\ (a+b)^1 &=& a+b\\ (a+b)^2 &=& a^2+2ab+b^2\\ (a+b)^3 &=& a^3+3a^2b+3ab^2+b^3\\ (a+b)^4 &=& a^4+4a^3b+6a^2b^2+4ab^3+b^4 \end{array} \)
I en el cas de les restes \((a-b)^n\):
\(\displaystyle \begin{array}{rcl} (a-b)^0 &=& 1\\ (a-b)^1 &=& a-b\\ (a-b)^2 &=& a^2-2ab+b^2\\ (a-b)^3 &=& a^3-3a^2b+3ab^2-b^3\\ (a-b)^4 &=& a^4-4a^3b+6a^2b^2-4ab^3+b^4 \end{array} \)
Exercici 17:
Espandeix les següents expressions fent servir la fórmula del binomi de Newton.
| a) \( \displaystyle \Big( x+4 \Big)^3 \) |
Solució: |
\( x^3 + 12 x^2 + 48 x + 64 \)
|
| b) \( \displaystyle \Big( 2x+1 \Big)^4 \) |
Solució: |
\( 16 x^4 + 32 x^3 + 24 x^2 + 8 x + 1 \)
|
| c) \( \displaystyle \Big( 3x-2 \Big)^4 \) |
Solució: |
\( 81 x^4 - 216 x^3 + 216 x^2 - 96 x + 16 \)
|
| d) \( \displaystyle \Big( x-\frac{1}{2} \Big)^3 \) |
Solució: |
\( \displaystyle x^3 - \frac{3}{2}x^2 + \frac{3}{4}x - \frac{1}{8} \)
|
| e) \( \displaystyle \Big( 4x+3 \Big)^5 \) |
Solució: |
\( \displaystyle 1024 x^5 + 3840 x^4 + 5760 x^3 + 4320 x^2 + 1620 x + 243 \)
|
| f) \( \displaystyle \Big( 5x^3-2x^2 \Big)^3 \) |
Solució: |
\( \displaystyle 125 x^9 - 150 x^8 + 60 x^7 - 8 x^6 \)
|
| g) \( \displaystyle \Big( x+\sqrt{2} \Big)^4 \) |
Solució: |
\( \displaystyle x^4 + 4\sqrt{2}\hskip 0.2em x^3 + 12\hskip 0.2em x^2 + 8\sqrt{2}\hskip 0.2em x + 4 \)
|
Exercici 18:
Determina el coeficient de \(x^4\) en el desenvolupament de \((x+3)^6\).
Solució:
\(\displaystyle \binom{6}{2} \cdot 3^2 = 135 \)
Exercici 19:
Determina el coeficient de \(x^2\) en el desenvolupament de \((x-4)^5\).
Solució:
\(\displaystyle -\binom{5}{3} \cdot 5^3 = -640 \)